n元字典序全排列与行列式定义公式

Written by Vam; Tuesday, Nov 9, 2021

n元字典序全排列

在我不了解任何算法的前提下，让我写出3个数的全排列，我会凭直觉写下：

4个数的全排列会多一些，但写出来也不费太大力气：

1234 1243 1324 1342 1423 1432
2134 2143 2314 2341 2413 2431
3124 3142 3214 3241 3412 3421
4123 4132 4213 4231 4312 4321

分析思路：

如果串只有1个元素，那么它只有1种排列：没有可以移动的元素
如果串有2个元素，那么它有2种排列： 1 2 与 2 1
如果串有3个元素，从最右侧开始，先把-1位置的元素移动到-2位置，到这里相当于完成了2元情况下的所有排列；
继续向左侧找，发现-3位置还有元素，那么把-2位置的元素移动到-3位置；
在上一步的基础上，再把-1位置的元素移动到-2位置；
……

元素: 1  2  3  4
     -- -- -- --
位置: -4 -3 -2 -1

如果串是“1 2 3 4”，把-1位置的元素移动到-3位置，不动的元素自动被挤到后面去，得到“1 4 2 3”。

把排列的流程继续画图做深入的分析：

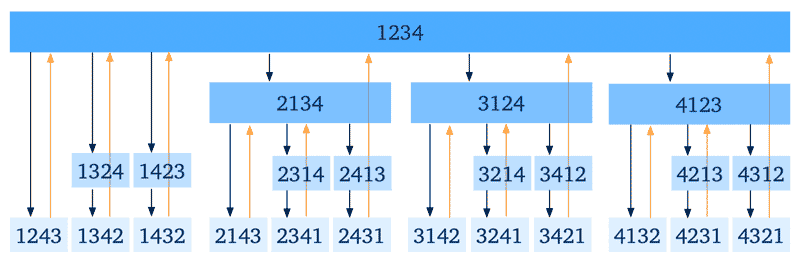
从上图能看出写出排列时的规律，如果把结果换成一个移动位置的函数 move(origin, target) ，可以得到下图：

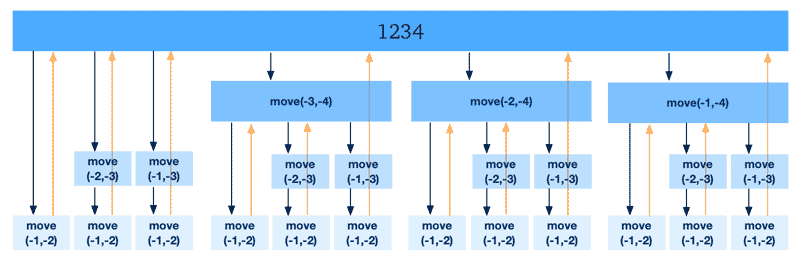
从上图可以看出一个明显的递归结构：先做2级的任务，发现有3级，要把它包含的2级的任务都做了，发现有4级，也要做3级、2级的任务……以此类推。

到这里就可以开始设计算法，但又发现一个问题，不论串是几元，都从最右侧开始移动，每当升到高一级，就又会从2元开始，造成图上有空缺的地方。这些地方如果写条件判断，会比较麻烦；那么换个角度，我能否补上一些操作？于是得到下图：

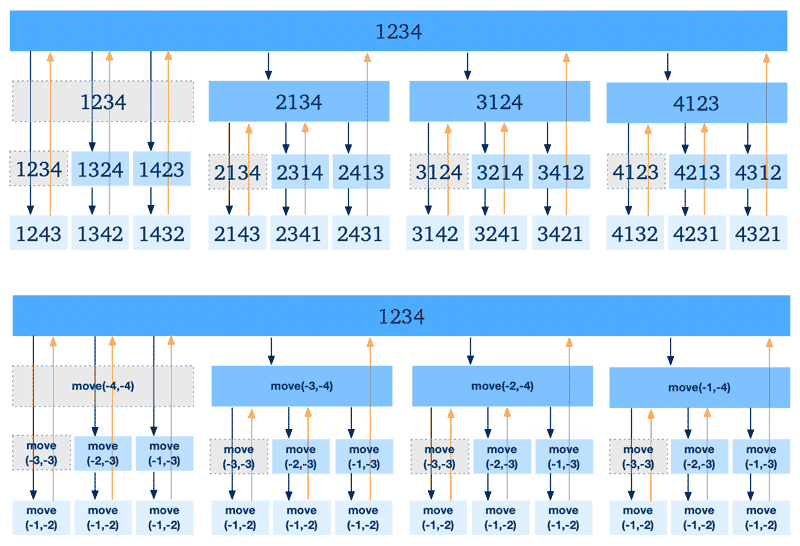
上图中灰色的操作是补全的，会发现它其实就是高阶坐标的位置与自己交换。

反过来想，我如果把一个1元串做全排列，它的结果只有一个，就是它自己，它的移动过程就是move(-1, -1)，也就等于什么都没做。也就是说1元串的全排列操作只有一次，我如果把1元串的全排列操作应用在任意长度的串上，这个串就是它自己。

补全以后，递归的逻辑简单了，但问题是会产生重复；解决重复的问题很简单，因为有一个很明显的条件可以判断 – origin 位置与target 相等。

到此逻辑清晰了，规则可以推广到n元，写代码：

行列式定义公式

很多教程都以3级行列式为范例：

$\begin{vmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{vmatrix}$

$= a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}$

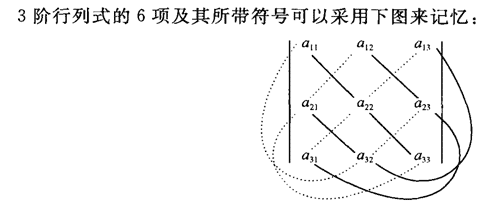
上面这张图，在视觉上对我有一定的误导性。3阶行列式的排列组合方法是先从左向右划斜线，再从右向左画斜线；如果4阶行列式也这样操作就不对了，因为n阶行列式的项的数量是n!个，也就是n的全排列的数量。

回到行列式的定义：

n阶行列式是n!的代数和，其中每一项是位于不同行、不同列的n个元素的乘积，把这n个元素以行指标为自然序列排好位置，当列指标构成的排列是偶排列时，该项带正号；是奇排列时，该项带负号。

$\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{21}& \cdots & a_{2n}\\ \vdots & \vdots & \vdots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} = \displaystyle\sum_{j_1 j_2 \cdots j_n} (-1)^{\tau(j_1j_2 \cdots j_n)} a_{1j_1}a_{2j_2}\cdots a_{nj_n}$

不考虑符号，先去考虑排列组合的问题，定义中的关键词是”……不同行、不同列的n个元素……”

现在我有一个4阶行列式，我开始写它的第一项，选取第一个元素，这时每个元素我都可以选择：

当我选定第一个元素是a11；开始选第2个元素，由于定义中要求“……不同行、不同列……”，那么a11所在的行与列就都不能成为第2个元素所选择的范围，第2个元素的可选范围是绿色部分：

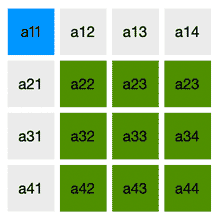
这也是为什么要“划掉a11的所在行与所在列……”；同理选择第二个元素为a22之后，可选范围如下：

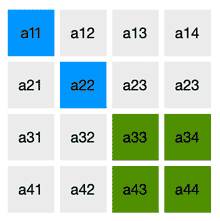
到这里也可以理解什么叫做“行列式按行（列）展开”。就是一行（列）中的每一个元素带领下的排列组合。

接下来画出4阶行列式所有的排列组合：

观察上图，发现了重要规律：4阶行列式的项的排列组合，它的列指标的变化就是4元串的全排列，而它的行指标是从1到4的循环，所以项数一共是4的阶乘个，即全排列的数量；行指标全都是顺序，不用考虑，列指标的逆序数决定了该项的符号。

有了这个规律，豁然开朗，开始写代码：

更改代码第7行变量 det_order 的值，就可以看到高阶行列式的视觉形式了。

Vam Works

Vam Works

n元字典序全排列与行列式定义公式